算法设计课期末考试，今天总结一些常用算法的原理和代码。本文实现的排序都是升序排序。（由于考试结束，算法总结待续）

一、冒泡排序（Bubble Sort）

1.算法步骤

（1）比较相邻元素：从列表的第一个元素开始，比较相邻的两个元素。

（2）交换位置：如果前一个元素比后一个元素大，则交换它们的位置。

（3）重复遍历：对列表中的每一对相邻元素重复上述步骤，直到列表的末尾。这样，最大的元素会被"冒泡"到列表的最后。

（4）缩小范围：忽略已经排序好的最后一个元素，重复上述步骤，直到整个列表排序完成。

2.动图演示

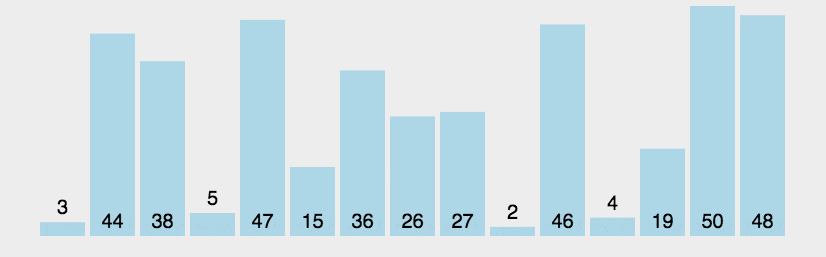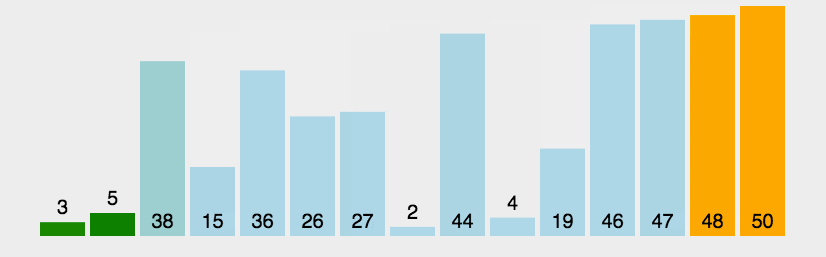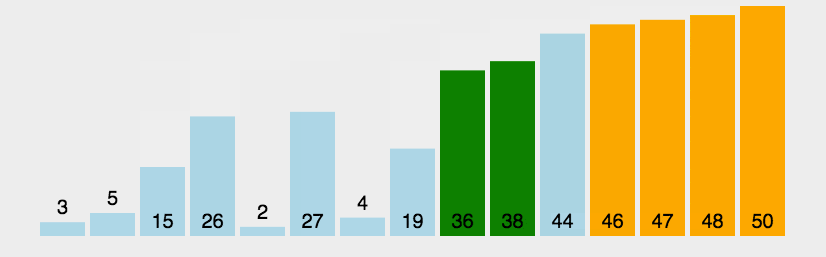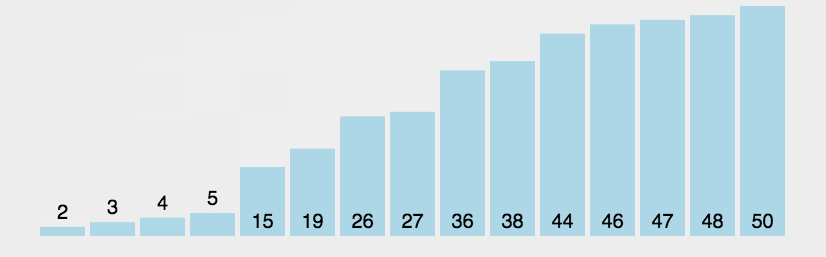
3.代码实现

def bubble_sort(_arr):
    for _i in range(len(_arr) - 1, -1, -1):
        for _j in range(_i):
            # 从左往右到最后一个未完成排序的数
            # 相邻两个数进行比较，将小的放前面，大的放后面
            if _arr[_j] > _arr[_j + 1]:
                temp = _arr[_j + 1]
                _arr[_j + 1] = _arr[_j]
                _arr[_j] = temp
    return _arr

4. 时间复杂度

最坏情况：O(n²)，当列表是逆序时。

最好情况：O(n)，当列表已经有序时。

平均情况：O(n²)。

5. 空间复杂度

O(1)，因为冒泡排序是原地排序算法，不需要额外的存储空间。

注：该算法是稳定的算法。

二、选择排序（Selection Sort）

1.算法步骤

（1）初始化：将列表分为已排序部分和未排序部分。初始时，已排序部分为空，未排序部分为整个列表。

（2）查找最小值：在未排序部分中查找最小的元素。

（3）交换位置：将找到的最小元素与未排序部分的第一个元素交换位置。

（4）更新范围：将未排序部分的起始位置向后移动一位，扩大已排序部分的范围。

（5）重复步骤：重复上述步骤，直到未排序部分为空，列表完全有序。

2.动图演示

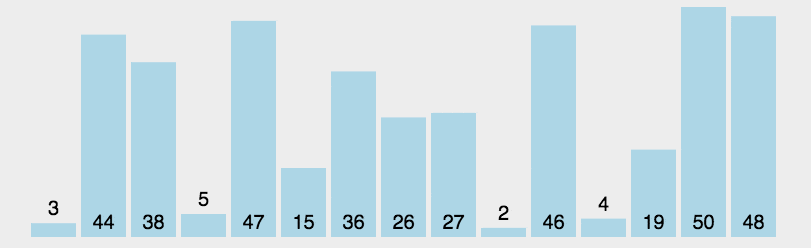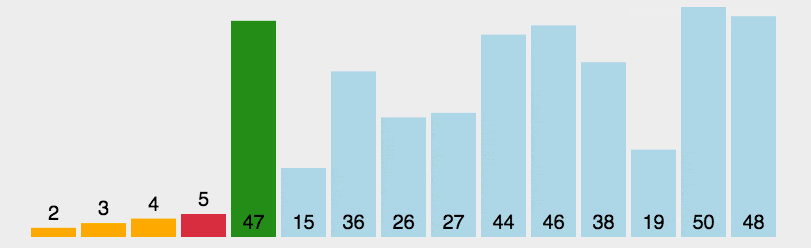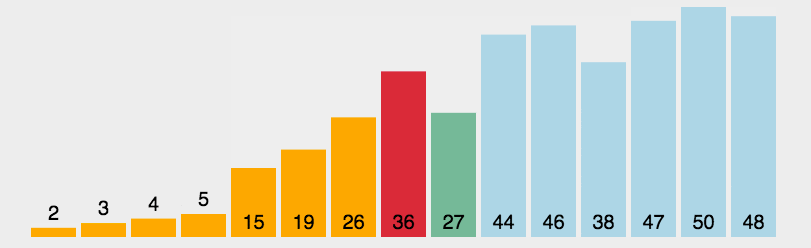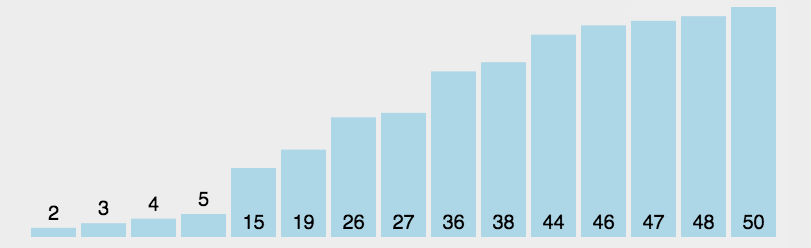
3.代码实现

def select_sort(_arr):
    # 用一个下标记录未排序元素的开始
    _index = 0
    while _index < len(_arr):
        # 找到未排序序列中的最小值，将其和未排序序列的第一个元素交换位置
        # 记录当前最小值的下标
        _min = _index
        _j = _index
        while _j < len(_arr):
            # 找到比当前最小值还小的元素，记录下标
            if _arr[_j] < _arr[_min]:
                _min = _j
            _j += 1
        # 当前已经找到未排序序列的最小值，将其和未排序序列的第一个元素交换位置
        if _index != _min:
            temp = _arr[_min]
            _arr[_min] = _arr[_index]
            _arr[_index] = temp
        _index += 1
    return _arr

4.时间复杂度

最坏情况：O(n²)，无论输入数据是否有序，都需要进行 n(n-1)/2 次比较。

最好情况：O(n²)，即使列表已经有序，仍需进行相同数量的比较。

平均情况：O(n²)。

5.空间复杂度

O(1)，选择排序是原地排序算法，不需要额外的存储空间。

注：该算法是不稳定的算法。

三、插入排序（Insertion Sort）

1.算法步骤

（1）初始化：将列表分为已排序部分和未排序部分。初始时，已排序部分只包含第一个元素，未排序部分包含剩余元素。

（2）选择元素：从未排序部分中取出第一个元素。

（3）插入到已排序部分：将该元素与已排序部分的元素从后向前依次比较，找到合适的位置插入。

（4）重复步骤：重复上述步骤，直到未排序部分为空，列表完全有序。

2.动图演示

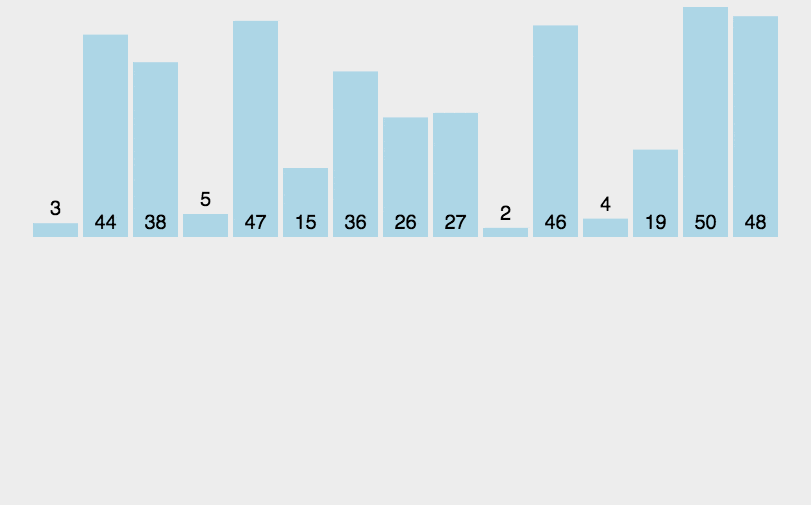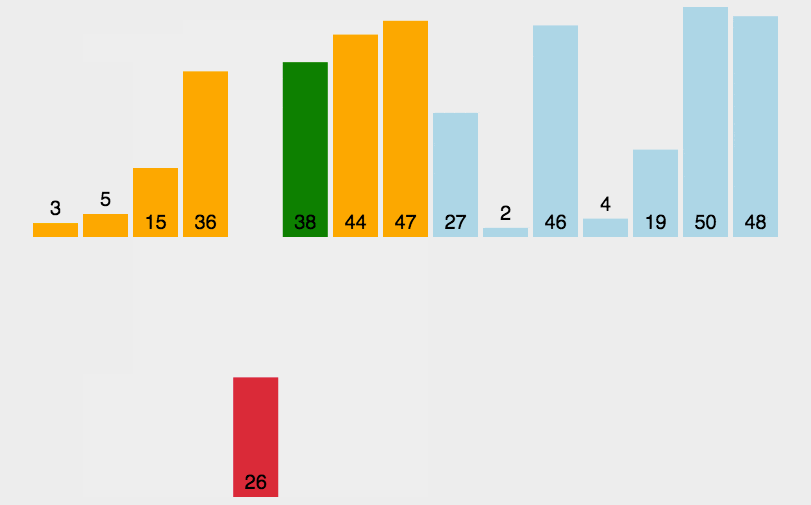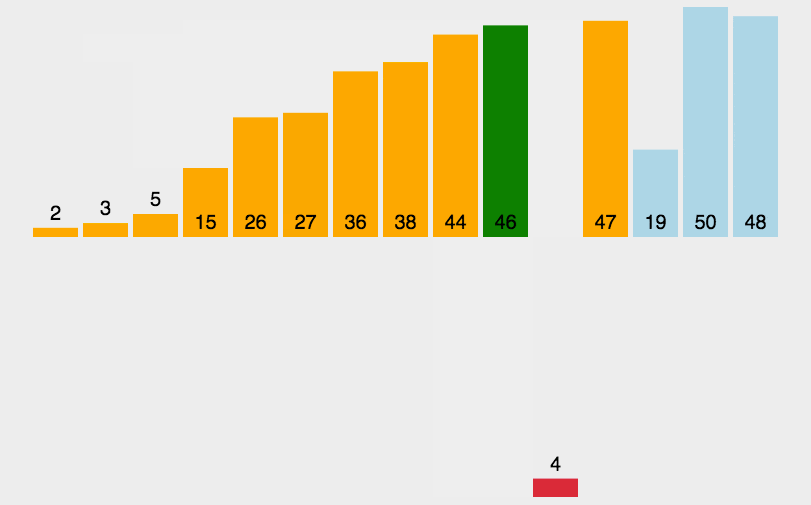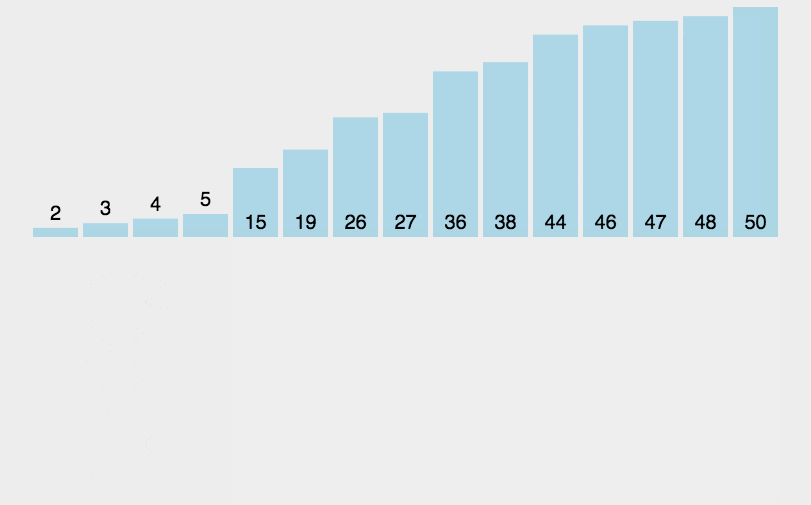
3.代码实现

def insertion_sort(_arr):
    # 遍历列表
    for _i in range(len(_arr)):
        # 遍历已经排序的序列，从右往左找，找到该元素合适的位置插入
        for _j in range(_i - 1, -1, -1):
            if _arr[_j] > _arr[_i]:
                # 找到需要插入的位置了，将这部分中间序列后移
                _temp = _arr[_i]
                for _k in range(_i - 1, _j - 1, -1):
                    _arr[_k + 1] = _arr[_k]
                _arr[_j] = _temp
    return _arr

4.时间复杂度

最坏情况：O(n²)，当列表是逆序时，每次插入都需要移动所有已排序元素。

最好情况：O(n)，当列表已经有序时，只需遍历一次列表。

平均情况：O(n²)。

5. 空间复杂度

O(1)，插入排序是原地排序算法，不需要额外的存储空间。

注：该算法是稳定的算法。